2023. 10. 23. 14:21ㆍR, 빅데이터 분석 실험
logistic regression analosis of massive data
테일러 급수를 사용하여 loglikelihood를 approximate 한다.(테일러 급수에 대한 설명은 수치해석학 카테고리에 있는 글에서 자세히 설명했다.)
기존의 테일러 급수와 다른건 행렬이기 때문에 다변량 테일러 급수로 근사해야한다.

다변량 테일러 급수는 다차원의 변수가 들어와도 1차원의 선형 함수로 근사해준다.
식을 분석해 다차원 변수가 들어와도 1차원 선형 함수가 됨을 이해해보자.
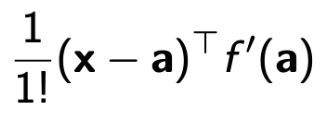
input에 해당하는 x는 우리의 예제에선 β이다. 또 β는 데이터셋이 N*P 행렬이라는 가정에서 종속변수 하나 빼고 intercept 넣어져서 p개 존재한다. 따라서 p*1차원이다.
테일러급수는 a는 근사하는 지점인데 x가 p차원인데 a도 p차원이여야한다. 따라서 (x-p)는 p 차원이다.
f'(a)도 생각해보자. f'(x) 는 p*1이여야한다. 결과 1개가 x0,..,xp의 선형결합으로 이루어져 p번 편미분을 해야한다.
그렇게 p개의 식을 가지게 된다. 또 각 항에대해서 생각해보면 x0 , x1 ,...,xp 의 선형결합으로 식이 이루어져 있고 여기에 a0, a1,...,ap를 넣은것이 f'(a)이니 결국 p*1 차원이다.
(x-a)^t * f’(x) 는 1*p , p*1 행렬을 곱하는거니 1차원이 된다.

f'(x)는 위에 서술해놓은것처럼 p개의 항에 각 항들이 x0 , x1 ,...,xp 의 선형결합으로 이루어져 각 항마다 p번 편미분 해야한다.
따라서 f''(x)는 p*p 행렬이 된다.
1*p,p*p,p*1 차원 행렬이 곱해져 결국 1차원이 된다.
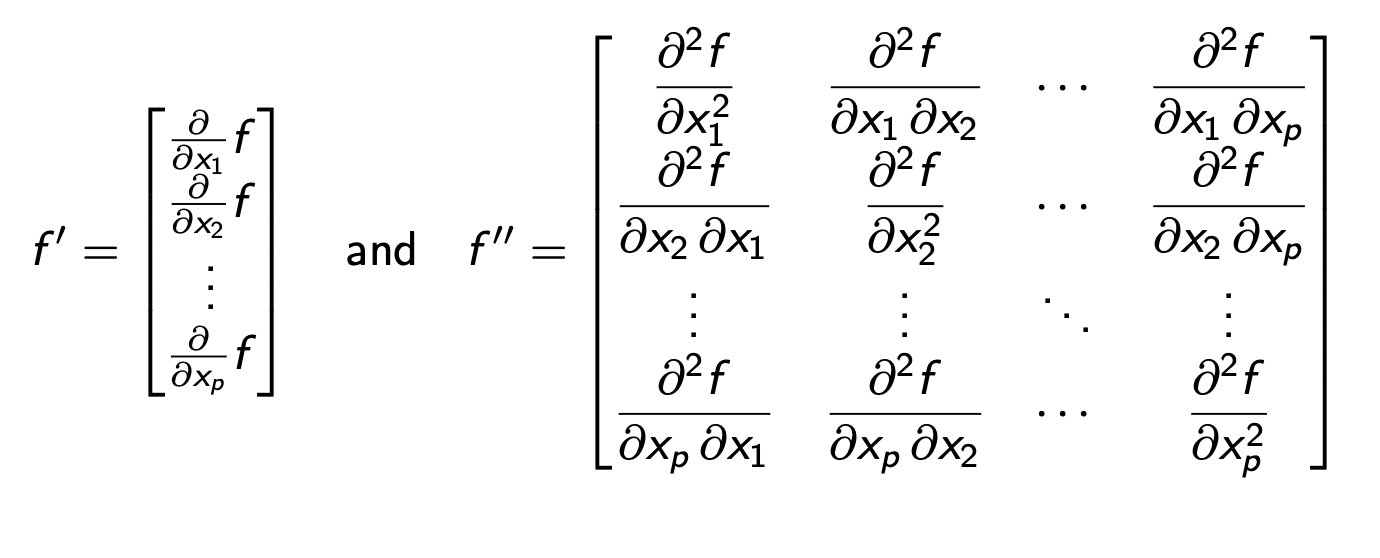
3차 도함수는 f''' 이 p*p 행렬이 p개있는거니 어떻게 1차원이 되는걸 보여야하나 싶겠지만 다행히도 아직은 구할 필요가 없다.
why? 우리는 테일러 급수에서 2차항까지만 사용할 것이기 때문이다.
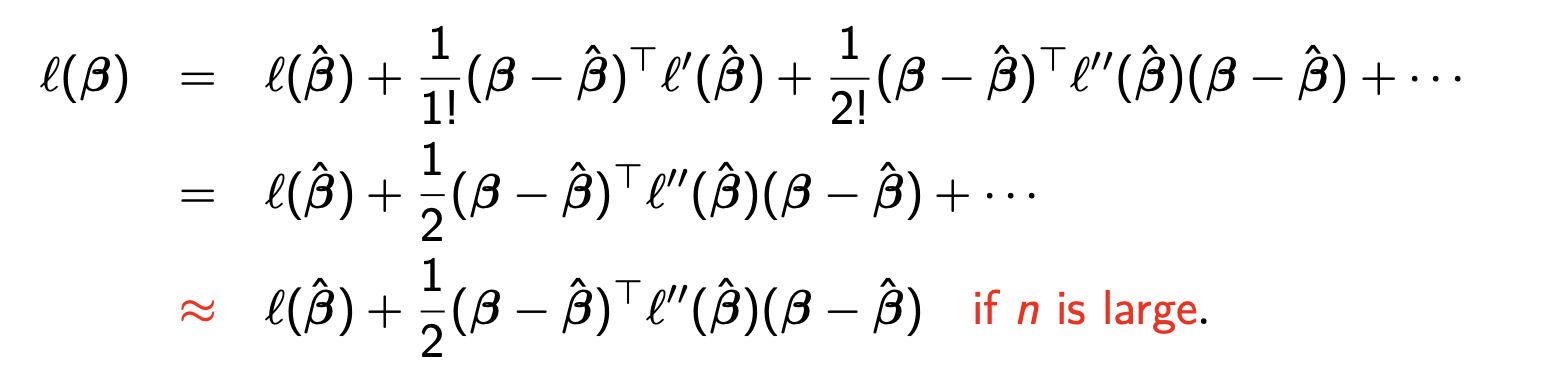
β^ 은 우리가 이전에 log.like함수로 대입하며 얻은 β의 추측값이다. 이를 다변량 테일러 급수로 나타내면 위의 식이 나온다.
1차 도함수가 들어간 항을 생각해보자. 우리는 L(β)가 최대가 되게하는, 즉 log.like(β)가 최소가 되게하는 β를 찾는 것이니
극소값이다. 따라서 우리가 식이 최소가 되게하는 β를 올바르게 찾았다면 1차 도함수의 값이 0이 된다.
그리고 3차 도함수 이상은 데이터의 행 개수 n이 충분히 크다면, 2차 도함수로도 충분하게 근사됨을 중심극한정리를 통해 증명할 수 있다고 한다. 따라서 3차 이상은 신경쓰지 않는다.

그래서 log.like 함수에 식을 최소화 시키는 β 를 넣는다면 위의 식을 계산한 것과 같은 결과가 나온다. β와 β^이 거의 같은 값이니 오른쪽 0나오고 log.like(β^) 이 나온다. (애초에 처음식도 log.like(β) = log.like(β) 이 나오지만 추후 데이터를 나눠서 나눌 수 있는지 확인할것이기 떄문에 식을 최대한 간소하게 만들었다.)
우리는 매우 큰 데이터임을 가정하니 L함수를 나눈다.
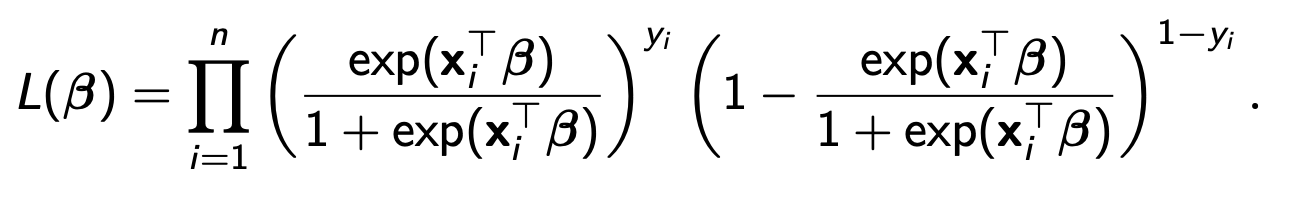
이식에서 생각해보면 파이 1부터 n/2의 결과와 파이 n/2부터 n까지의 결과가 같으니까 L함수를 나눠도 상관이 없다.
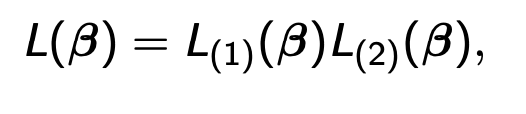
그리고 데이터를 나누기전 테일러 급수로 표현한 Log.like에서 2차 도함수 항을 행렬로 나타내보자

A는 f''(β^) , b = f''(β^)β^ 일 때 다음이 성립한다.
이 식에서 A를 n등분 나눈다면 아래의 식을 만들 수 있다.
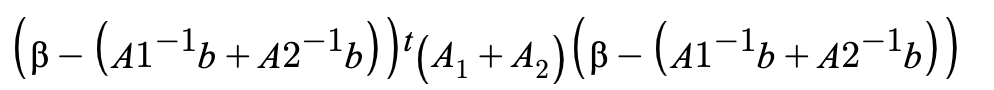
A^-1b 는 p*1 행렬이고 A1^-1b , A2^-1b를 각각 더한 값과 같다.
A는 p*p행렬이고 이계도함수이다. A1 에서 이계도함수를 구하면 p*p 행렬이고 A2도 p*p 행렬이며 A는 이둘을 합한것과 같다.
따라서 위의 식이 성립하는데 우리가 궁금한건 데이터를 나눴을때 β^이 어떻게 나눠지는가가 궁금한 것이다.
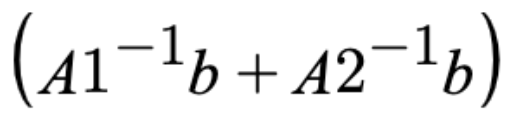
β^은 위와같고 우리가 데이터를 나눠 각각의 f(β1^) 과 f(β2^) , β1^,β2^ 을 구한다면 나중에 위의 식으로 합칠 수 있다는 것을 알게되었다.
이를 통해 online update, massive data problem 을 해결할 수 있게 되었다!
여기서 주의할 점은 우리는 데이터 n의 개수가 많기 때문에 테일러 다항식으로 표현할 때 3차 도함수 이후를 다 버렸다.
n이 작다면 위의 과정이 성립하지 않고 또 각각의 데이터로 f(βk^) 와 βk^를 구하는데 이 각각의 데이터가 작다면 테일러 급수로 인한 근ㄴ사가 성립하지 않기때문에 위의 식이 성립될 수 없다.
'R, 빅데이터 분석 실험' 카테고리의 다른 글
| [R] logistic regression anlysis of mass data (1) | 2023.10.23 |
|---|---|
| high dimensional data (1) | 2023.10.23 |
| method to find β of logistic regression anlysis (1) | 2023.10.22 |
| [R] 로지스틱 회귀 분석 실습 (0) | 2023.10.22 |
| 로지스틱 회귀 분석 (0) | 2023.10.21 |