2023. 10. 21. 23:27ㆍR, 빅데이터 분석 실험
방금까지는 종속 변수가 연속적인 값이었다.
각각의 독립변수와 종속변수의 관계식을 만들고 해당 관계식에 독립변수의 값을 넣는다면?
종속변수가 몇일지 예측할 수 있었다.
'주식의 시가가 60000원이고 최고가가 70000원이었으니 주식의 종가가 71230원일 것이다'처럼 예측할 수 있었다.
하지만 시험 점수에 따른 불합격 여부를 예측하라고 한다면 이러한 선형 회귀가 예측할 수 있을까?
종속 변수는 1(합격), 0(불합격) 뿐이다.
답은 절대로 사용하면 안된다.
why? 선형 회귀 모델은 확률을 예측하도록 설계된 모델이 아니라 값을 예측하도록 설계된 모델이기 때문이다.
가능한 결과 값(종속 변수)의 값이 (-INF, INF) 이다.
따라서 가능한 결과값이 (0, 1) 사이가 되도록 모델을 설계해야한다.
베르누이 분포를 고려해보자
P(y=1) = p // 합격할 확률 p
P(y=0) = 1-p // 합격하지 못할 확률 1-p

이를 토대로 해당 식을 세울수있다. y가 1이라면 p , y가 0이라면 1-p
E(Y) 는 y의 평균이고 np 로 구할 수 있는데 1번 시행하니까 E(y) = p 가된다.
E(Y) = g(X) 로 정의하자.
즉 독립변수를 g에 넣으면 Y의 평균이 나온다.
E(Y) = g(x) = p
여기서 p는 (0,1) 사이의 값이다.
만약 E(y) = β0 +β1x1 +β2x2 +···+βnxn 라고 가정한다면 E(y)의 범위는 (-INF, INF) 가 되니 적절하지 않다.
따라서 E(Y)= g(x)를 아래와 같이 정의한다.

why??
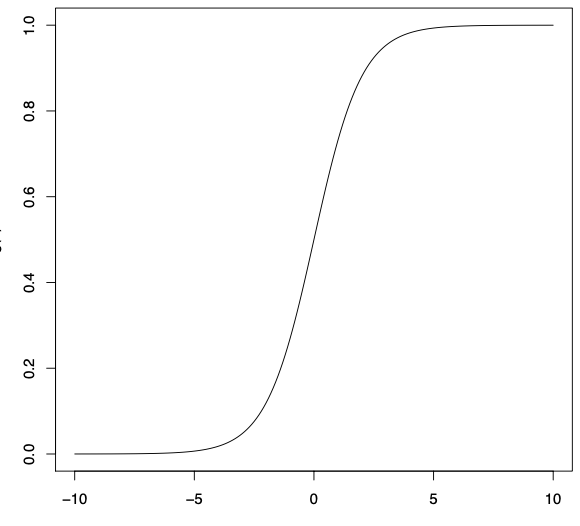
그렇다면 E(y)의 범위가 0과 1사이이다.
β0 +β1x1 +β2x2 +···+βnxn 를 g(x)에 대입하면 [0,1] 범위에서 값이 나오니 바른 모델이라고 할 수 있다.
그래서 g(x) 에 β0 +β1x1 +β2x2 +···+βnxn 를 대입하면 E(Y)가 나온다.
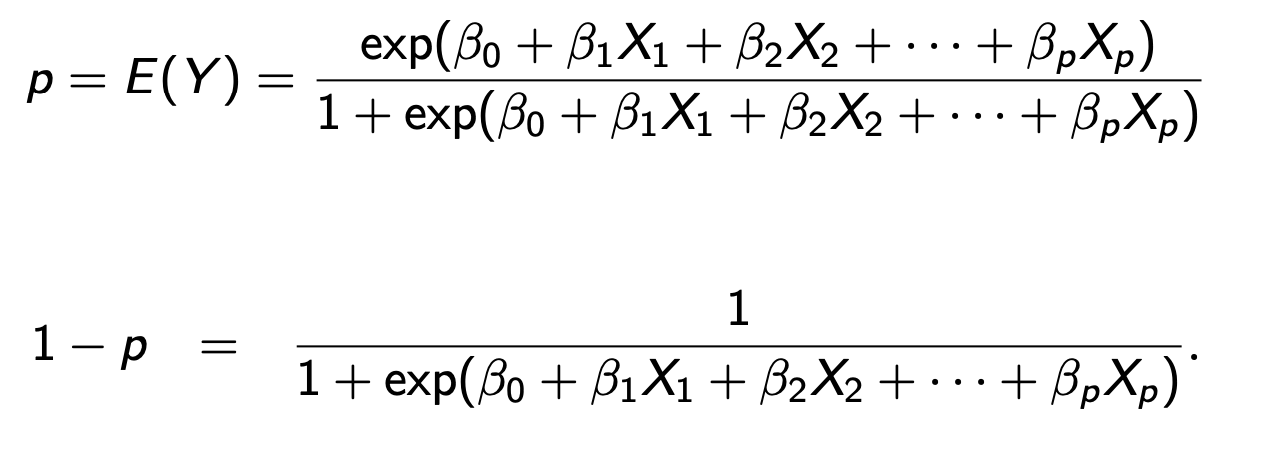


또 해당 과정을 통해 E(Y) = p 에서 β0 +β1x1 +β2x2 +···+βnxn 빼낼 수 있고 β0 +β1x1 +β2x2 +···+βnxn 의 p에 대한 식이
ln(p/1-p) 임을 알 수 있다.

우리가 결국 구하고자하는 것은 g( β0 +β1x1 +β2x2 +···+βnxn) = p 에 대해서 최적의 β0 ,β1 , ... ,βn 을 구하는 것이다.
이를 어떻게 구할 수 있을까?
가능한 Y들의 pmf의 곱을 구하는 likehood function을 사용한다. 각 데이터에 해당 데이터에 가장 적합한 확률 p가 무엇인지 찾는지가
우리의 목표이다.

우리는 이전의 과정을 통해 p가 시그모이드 함수에 Xb(행렬 표현) 을 대입한 값과 같음을 안다. (아래의 그림 xi^t 는 X의 i번째 방정식를 열벡터를 transpose 한 것.)
이를 대입하여
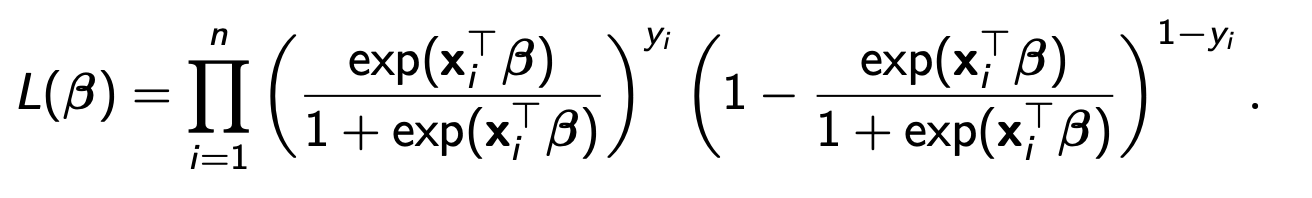
해당 식은 각 방정식(X를 구성하는 X의 i번째 행들)에 대해 Y(성공 or ,실패)에 따른 곱을 각각 곱하는 식이다. 이 식이 최대가 된다는건 무슨의미일까? 이를 이해하기 위해서 likelihood에 대한 이해가 필요하다.
likelihood는 가능도를 나타낸다. 10번의 동전을 던져서 7번이 앞면이 나왔다면 앞면이 나올 확률이 몇일때가 가장 설명하기 좋을까?
답은 0.7 이다. 확률이 0.7 일때 pmf 가 가장 높게 나오기 때문이다.
하지만 질문을 바꿔서 10번 시행을 했는데 1번째 시행은 10번의 동전을 던져서 1번 앞이 나왔고 , 2번쨰 시행은 10번의 동전을 던져서 2번 앞이 나왔고 ... 10번째 시행에서 10번의 동전을 던져서 10번 앞이 나왔다.
이때 앞면이 나올 확률이 몇이어야 이 경우를 설명하기 좋을까? 답은 1/2 이다 . p가 0.1일 때 각 시행에 대한 pmf의 곱을 한것, p가 0.2 일때 각 시행에 대한 pmf의 곱을 한것 등 모든 경우를 비교해 봤을때 p가 0.5일때가 가장 각 시행에 대한 pmf의 곱이 높기 때문이다.
이를 MLE라고 하고 그래서 위의 설명에서도 각 방정식에 대한 성공, 실패 확률의 곱이 가장 커지는 구간에서 b가 각 방정식의 경우를 가장 잘 설명한다고 말할 수 있게되는 것이다.
그래서 결론적으로 위의 식을 최대로 만드는 b를 구하는 것이 우리의 과제이다.
'R, 빅데이터 분석 실험' 카테고리의 다른 글
| method to find β of logistic regression anlysis (1) | 2023.10.22 |
|---|---|
| [R] 로지스틱 회귀 분석 실습 (0) | 2023.10.22 |
| [R] online updating problem (1) | 2023.10.21 |
| massive data는 어떻게 선형회귀분석을 적용할까? (1) | 2023.10.21 |
| linear regression analysis (1) | 2023.10.21 |