체비쇼프 다항식

체비쇼프 다항식

 

cos^-1(cos θ) = θ 를 이용해 cos(nθ) 를 만든다.

삼각함수 덧셈 정리를 통해 다항식을 유도해 낼 수 있다.

 

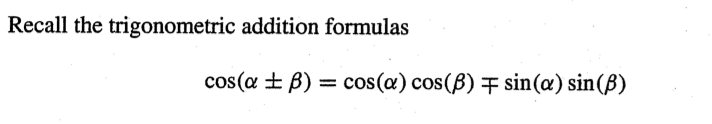
일반항 유도 매우 중요

점화식을 이용해 Tn을 구할 수 있음

 

체비쇼프를 왜 사용하는가?

사용할 수 있는 조건 : -1<= x <= 1 (cosθ 라서 이 범위안에서만 가능)

만약 -1과 1이 아니라면 x를 z로 치환해 -1<=z<=1 에서 구하고 다시 x로 변환한다.

 

이를 논하기전 변수 선택에 대해 이야기하겠다. 우리가 흔히 보간을 하는데 점이 주어져있다. 근데 만약 주어진 구간안에서

오차가 가장 적게 되는 점을 능동적으로 선택해야하는 경우 체비쇼프가 매우 효과 적이다.

아까 x를 cosθ 으로 정의했으니 다음을 만족한다.

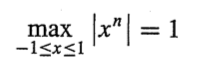
위의 특성 때문에 n이 증가하더라도 최대 크기가 변하지 않는다.

Tn의 x^n 항의 계수를 1로 만들면 (최고차항의 계수가 1인 방정식을 monic polynomial 라고 함)

-1<= x <= 1 에서 가장 작은 최대값을 가지는 일원 다항식은 1/2^n-1*Tn이다. 이때 최대값은 1/2^n-1 이다.

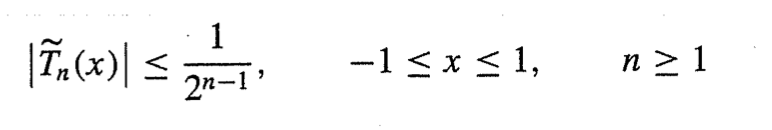
분할 차분법에서 e(x) =(x-x0)(x-x1)…(x-xn)f^(n+1)(cx)/(n+1)! 이었는데 (x-x0)(x-x1)…(x-xn) 이부분을 체비쇼프 방정식을 통해 근을 선택한다면? 아주 효과적으로 오차를 줄일 수 있다.

 

또 체비쇼프 방정식의 근은 수열형태로 나타난다는 특성이 있다.

T4(x) = cos(4θ), x = cos(θ)

cos(4θ) = 0을 만족해야함

4θ = +-π/2 , +- 3π/2 , ... (수열형태로 나타남)
θ = +-π/8 , +- 3π/8 , ... (수열형태로 나타남)

 

x= cos(θ) = cos(π/8),cos(3π/8), ...

 

해당 점들로 e^x를 근사한다면? -1과 1 구간에서 성능이 매우 좋다. 

 

 

 

분할 차분법에서 e(x) =(x-x0)(x-x1)…(x-xn)f^(n+1)(cx)/(n+1)! 이었는데

(x-x0)(x-x1)…(x-xn) 이부분을 체비쇼프 방정식을 통해 근을 선택한다.