2023. 10. 17. 23:35ㆍ수치해석학
일차 근사함수 p1(x)
p1(a) = f(a)
p1’(a) = f’(a)
p1(x) = β1x + β2
= β1(x-a) + f(a)
= f’(a)(x-a) +f(a)
-> p1(x)’ 미분하고 a를 대입하면 상수항빼고 다 0이 되서 상수항인 β만 남음
이차근사함수 p2(x)
p2(a) = f(a) / 한점을 결정,
p2’(a) = f’(a) / 기울기
p2’’(a) = f’’(a) / 곡률
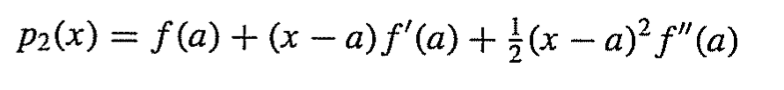
- taylor approximations
미분, 적분하기 너무 어려운 함수들이 있음.
(e^at , sin at, cos at etc)
이때 우리가 풀기쉬운 다항식으로 근사한다면 쉽게 적분하고 미분하여 문제를 해결할 수 있지않을까?
g(x)라는 근사 함수를 정의하기위해 3가지가 필요하다.
tangent , curvature, torsion 를 알아야함
이를 구하기 위해 f’(a) f’’(a) f’’’(a) 의 근사치를 알아야함.
g(x,y) 가 이차식 + a’x^2 + b’xy + r’y^2 + ? 의 형태일때 일차식은 기울어진 정도에 , 이차식은 얼마나 오목한가에 대한 정보를 나타냄.
p1(a) = f(a) // 일차 근사함수
a 지점에서 선형으로 근사한 것을 의미한다.
예를 들어 x =0 일 때 f(x) = e^x 를 p1(x) 로 근사해보자.
p1(0) = f(0) = e^0 = 1
p1’(0) = f’(0) = e^0 = f’(0) = 1
p1 = 1/1!(x-0) + 1 = x+1
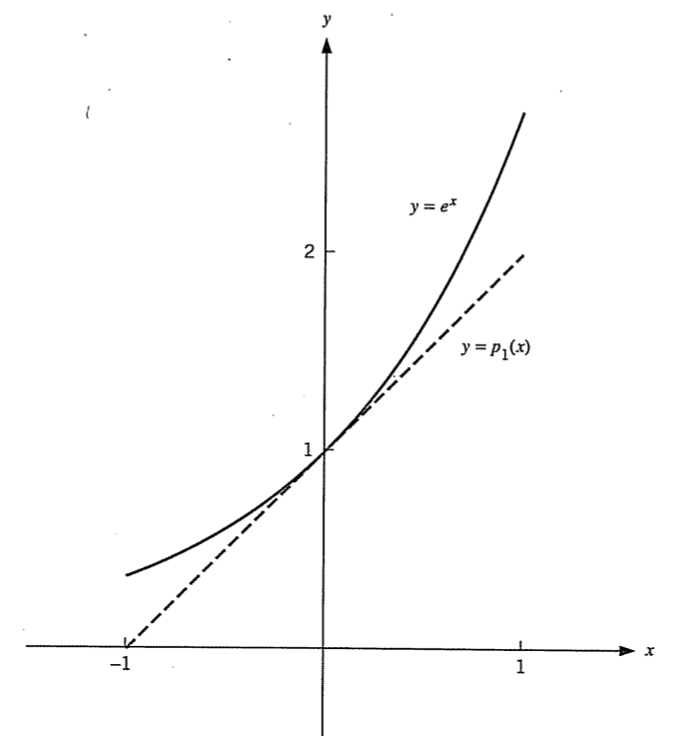
f’(0) 를 사용해 곡률, 비틀림없이 기울기만 표현하는 근사함수가 완성 됐다.
계속해서 p2를 구해보자.
p1(0) = f(0) = e^0 = 1
p1’(0) = f’(0) = e^0 = f’(0) = 1
p1’’(0) = f’’(0) = e^0 = f’(0) = 1
p2(x) = 1/2! (x-0)^2 + 1/1!(x-0) + 1 = 1/2x^2 + x + 1
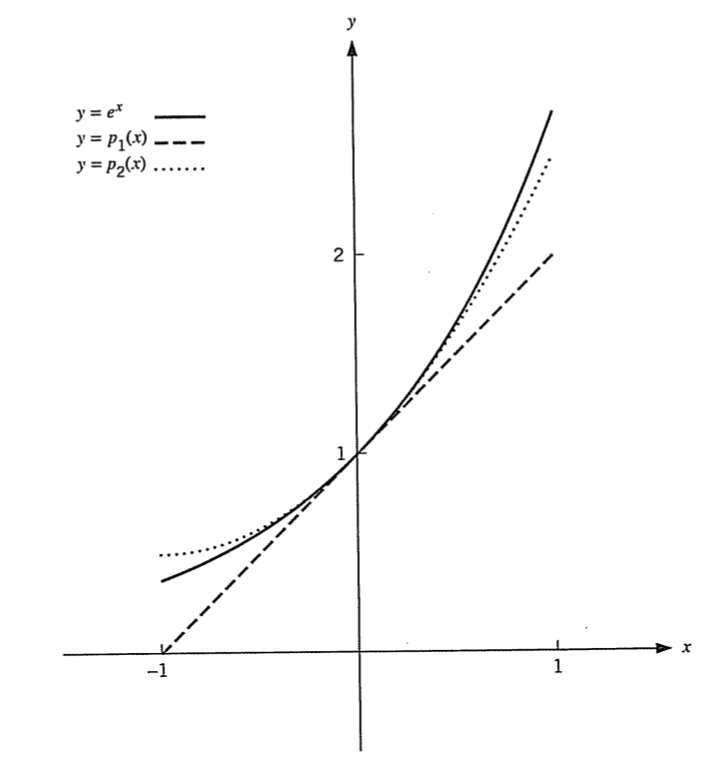
f’’(0) 를 사용해 곡률이 추가 된 근사를 했다.
여기서 중요한건 0 근처에서는 근사 되는걸로 보이지만 0에 멀어지면 멀어질수록 잘 근사 되지않는다.
이제 이를 통해 다차항 근사를 알아보자.
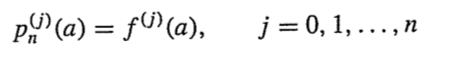
위 표기의 의미는 j번 미분한 n차 근사함수의 a에서의 값이다.
j derivative (j 도함수)
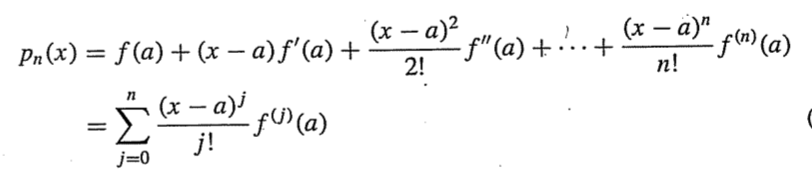
미분을 할때마다 차수가 곱해지니 횟수!을 나눠줘야 항의 계수를 알 수 있다.
ex) 3x^3 을 3번 미분하면 3*3*2*1 = 18 이 되는데 우리가 원하는건 이 3을 뽑아내는거니 3!을 나눠준다.

a 지점에서 근사한 n차 테일러 다항식
ex)
a = 0 일때 테일러 급수 표현
f(x) = 3x^2+2x +4
f(0) = 4
f’(x) = 6x +2
f’(0) = 2
f’’(x) = 6
f’’(0) = 6
이를 테일러 다항식 형태로 나타내보면
f(x) =f(0) + f’(0)/1! (x-0)+ f’’(0)/2! (x-0)^2 = 4 + 2x +3x^2
a = 3 일떄 테일러 다항식 표현
f(x) = 3x^2+2x +4 = 3(x-3)^2 +20(x-3) +37
f(3) = 37
f’(x) = 6(x-3) + 20
f’(3) = 20
f’’(x) = 6
f’’(3) = 6
f(x) =f(3) + f’(3)/1! (x-3)+ f’’(3)/2! (x-3)^2 = 37 + 20(x-3) + 3(x-3)^2
이 예제를 통해 f''(0)/2! 가 우리가 근사할 함수의 x^2의 계수임을,
또 f^(n)(x)/n! 이 우리가 근사할 함수의 x^n의 계수임을 감잡기를 바란다.
요약
*좌변과 우변이 모든 x에 대해 같은 것이 아니라 x = a 근처에서만 성립한다는 점.
*0차 도함수는 근사할 위치, 1차 도함수는 기울기 , 2차 도함수는 곡률 , 3차 도함수는 비틀림을 표현
(tangent , curvature, torsion)
*만약 f^(n)(x) = 0 이라면 pn(x) 는 n차보다 더 작은 차수를 가질 수 있다.
'수치해석학' 카테고리의 다른 글
| 체비쇼프 다항식 (1) | 2023.10.26 |
|---|---|
| the error in taylor’s polynomial, polynomial evaluation (0) | 2023.10.18 |