the error in taylor’s polynomial, polynomial evaluation

f(x) 에 대한 테일러 근사를 효율적으로 사용하려면 정확도 계산하는 과정이 필요하다.

 

1. taylor's remainder thm

f(x)가 A<= x <=B 인 구간에서 연속인 n+1개의 도함수를 가진다고 가정.

이 구간 사이에 있는 점을 a라고 하자.

 

 f(x) - pn(x) 를 Rn로 정의하자.  (Pn은 a를 기준으로 근사됨.)

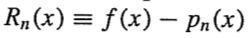
f(x)에 n개의 도함수들로 근사한 pn(x)를 빼면 n+1 번째 도함수가 남고 이는 f^(n+1)(a)/(n+1)! (x-a)^(n+1) 이다.

그러면 Rn(x)는  f^(n+1)(a)/(n+1)! (x-a)^(n+1) < Rn(x) <  f^(n+1)(x)/(n+1)! (x-a)^(n+1) 을 만족한다.

a와 x 사이의 임의의 값 cx를 둬서 Rn(x)를 정의하면 밑의 식을 얻을 수 있다.

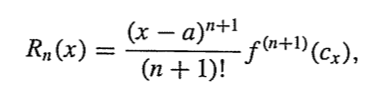
이를 활용해 보자.

f(x) = e^x 이고 a= 0 , x = 1 일때, Rn(1)가 어느 범위의 값인지 알아보자

e^x - pn(x) = e^c/(n+1)! x^n+1 , n>= 0 ,  0(a) < c < x 

x = 1

0 < c < 1

e^x - pn(1) = e^c/(n+1)!

c가 0일때와 1일때의 값 사이에 Rn(1) 이 존재한다.

1/(n+1)! < Rn(1) < e/(n+1)!

 

Rn(1) 이 10^-9 보다 작은 오차를 가지기 위해 n이 몇 이상이 되어야하는가?

 

e/(n+1)! 는 계산하기 불편하니 e보다 큰 자연수를 찾자.

e<3 이고  e/(n+1)! < 3/(n+1)! 임을 알 수 있다.

 

1/(n+1)! < Rn(1) < e/(n+1)! < 3/(n+1)!

 

여기서 우리는 가정을 통해 Rn(1) 이  10^-9 보다 작은 값이라고 생각하자.

Rn(1) <= 10^-9

 

Rn(1)를 모르지만 상한을 아니 상한울 10^-9 보다 작다고 가정하자.

3/(n+1)!  <= 10^-9 

n >=12 일때 해당 부등식을 만족한다.

따라서  R12(1) < 3/(12+1)! <= 10^-9 임을 알 수 있다.

p12(1) 은 0<c<1 일때 10^-9보다 작은 오차를 가지는 근사임을 알 수 있다.

또 n이 무한에 가까워질수록 오차는 0에 가까워짐을 할 수 있다.

 

*f(x)의 고계도 함수가 연속임을 가정해야함

 

용어 정리

테일러 다항식 -> 도함수 n까지

테일러 급수 ->  도함수 무한까지

 

ex)

e^x를 0에서 근사시켰을 때 테일러 급수

 

 

polynomial evaluation

프로그래머 관점으로 다항식을 평가하자.

 

p(x) = a0 +a1x + a2x^2 + …. + anx^n

a0 , .. , an 과 x가 주어질때 몇번의 곱셈으로 다항식을 계산할 수 있을까?

 

p(x) = 3 - 4x -5x^2 -6x^3 +7x^4 - 8x^5

각 항을 c*x^k  으로 계산한다면

p(x) 를 평가하기 위해 1 + 2 + 3 +4 +5 (5*6 /2)의 곱셈이 필요하다.

4*x(1) + 5*x*x(2) + …

O(n^2)

 

어떻게 더 효율적으로 다항식을  평가할 수 있을까?

 

x^k = x * x^(k-1) 로 보자

x부터 순차적으로 보면서

x 

x*x 

x*x^2 // 여기서 x^2은 이전에 계산

그러면 1+2+2+2+2 의 곱셈이 필요하다.

O(2n-1)

 

 

또 다른방법 nexted multiplication

3+x(-4 +x(-5 +x(-6 +x(-7 +8x) )))

이러면 O(n) 가능

 

고속 푸리에 변환, 점화식을 이용한 방법 등을 이용해 더 효율적으로 다항식을 평가할 수 있다.