2023. 12. 20. 22:19ㆍ카테고리 없음
——————
가우스 소거법 룰
- interchange two equation (행 변환)
- multiply a nonzero contant a to a equation (0이 아닌행 곱하기)
- addtion of a nonzero multiple of one equation to another equation (0이 아닌 행의 곱으로 다른 행 0 만들기)
3가지를 통해 가우스 소거법을 시행할 수 있다.

전진 소거법과 후진 대입의 반복

1행의 x1배 + 2행의 x2배 + 3행의 x3배의 합.
즉 선형결합으로 행렬곱을 바라보자
가우시안 소거법의 공식화
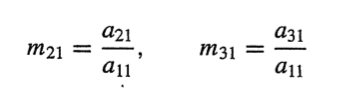
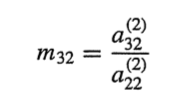
E(2) - m21*E(1) =
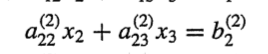

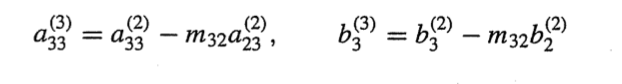
후진 대입법

컴퓨터 공학적으로 이를 구현하면 O(n^3) 이 나온다. i , j , k 필요

적용해보기

partial pivoting
방정식을 풀기위해 우린 10진법 컴퓨터로 부동 소수점을 사용해서 방정식을 푼다.
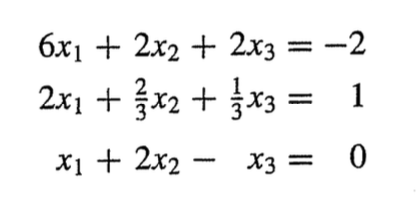

왼쪽 식이 오른쪽 행렬로 표현된다.
문제는

대각성분이 계산상은 0이어야하는데 부동소수점 방식의 한계로 완전한 0이 아닐 수 있다.
이러한 rounding error를 방지해야한다. 단순한 방법은 2행과 3행을 바꿔 전진 소거를 진행하는 것이다.
그럼 m32 가 0.0001/1.667이 나오고 원래 나와야할 해에서
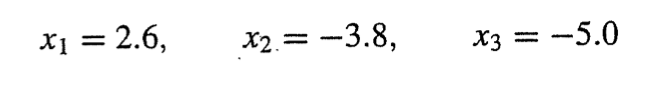

작은 오차가 생기게된다.
이 방식을 수식화 해보자(부분 피벗팅:pivot element로 0과 가까운 계수를 피하는 방법)
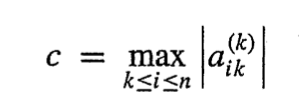
대각 akk 을 k~n까지의 행중 k열의 값이 가장 큰 행과 교환한다.
c와 새로운 akk가 같아지도록 만든다. 이때 akk 를 pivot element라고 부른다.
——————————
역행렬 아이디어
AX = I
에서 3*3행렬 X가 A의 역행렬이다.

해당 식에서 I를 1개의 열 씩 나눈다.
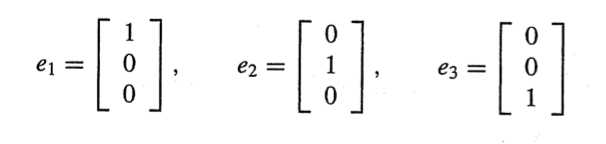
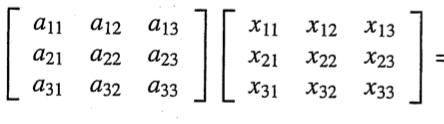
의 3*3 결과 행렬의 1번째 열행렬은

위의 식을 만족한다.
Ax = [1 0 0]^t
의 결과를 만족하는 벡터 x는
역행렬의 1열을 의미하게 된다.
즉

를 만족하고
[x.1 , x.2, x.3 ]이 A의 역행렬이 된다.
이를 응용해보자.

[x1 x2 -x3 ;x1 2x2 -2x3 ; -2x1 x2 x3] 행렬 A로 생각하자.
A = I이고 여기서 가우스 소거법을 이용하여
[x1 x2 -x3 ; 0 x2 -x3 ; 0 0 2x3] = [1 0 0 ; -1 1 0 ; 5 -3 1] 를 구한다.
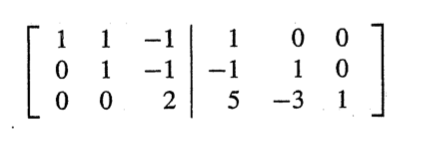
여기서

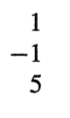
이 두부분을 따로 떼서 본다.(Ax = b꼴로 보자)
위 식을 만족하는 x는 A의 역행렬의 첫번째 열이 된다.
그리고

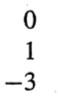
이 두부분을 따로 떼서 본다.(Ax = b꼴로 보자)
위 식을 만족하는 x는 A의 역행렬의 두번째 열이 된다.
또 기존 A를 I를 만든다면 역행렬이 구해진다.
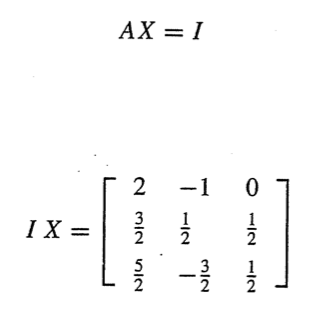
—————————
첨가행렬을 이용한 역행렬 구하기
참고)
가우스 조르단 소거법을 활용한 역행렬 구하기
https://blog.naver.com/agnes0129/203468722
참고)
기본행렬의 역행렬
https://angeloyeo.github.io/2021/06/15/elementary_square_matrices.html
가우스 조르단 소거법을 활용하여 역행렬을 구하면
E[A I] = [EA EI] 가 되는데
E가 A^-1라면
[I A^-1]가 된다.
———————————————————————————
Operation count
U는 상 삼각행렬
g를 우항 벡터로 표현
시그마 공식
https://m.blog.naver.com/biomath2k/221847659166

step 1에 대해 생각해보면
[1 2 3; 1 4 4;1 5 6]
2행과 3행에 1행을 빼야한다.
각 행의 첫열은 어짜피 0이 되니까 무시하고
각 행의 2열 3열을 빼줘야한다.
2^2 의 빼기가 발생한다.
근데 막빼면 안된다.
곱하기의 경우 각 행을 뺄때 2행은 1행 요소에 m21을 곱한걸 빼야하고,
3행은 그 결과에 m31를 곱한걸 빼야한다.
4번의 곱하기가 발생한다.
m21을 구하기 위해 a21/a11
m31을 구하기 위해 a31/a11
2번의 나누기가 발생한다.
step2도 동일한 방식으로 계산할 수 있고 step2를 통해 상 삼각행렬을 얻을수있어 계산이 끝난다.
이를 시그마 연산을 통해
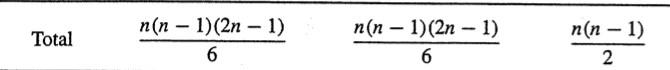
를 이끌어낼 수 있다.
시그마 (k-1)^2
시그마 (k-1)
계산하기

더하기 빼기 연산 횟수 AS
곱하기 나누기 연산 횟수 MD
결과항 b->g에 대한 연산 횟수를 계산하자.
이전 행렬은 2번의 행빼기 , 각 행에 대한 열빼기로 제곱연산했는데
결과같은 경우 행연산만해주면 되니 step1에서 n-1의 연산이 발생
곱하기 경우도 각 행을 뺄때 m21 과 m31을 한번씩 곱하면 되니 n-1의 연산 발생
나누기 같은 경우 행렬 연산에서 m21과 m31을 구하니 결과에선 신경쓸게 없어 0번 발생
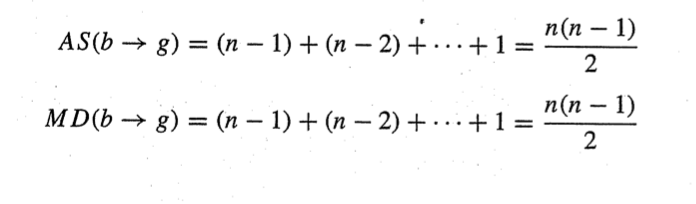
를 유도할 수 있다.
마지막 후진 대입법을 생각해보자
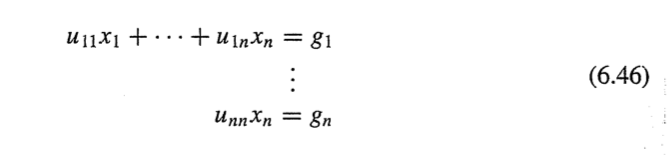
xn을 구하기 위해 계수 unn을 나눠야해서
1번의 나누기 발생
xn-1을 구하기 위해
un-1 * xn-1 + un-1n xn = gn-1
un-1*xn-1 = gn-1 - un-1n*xn 한번의 빼기가 발생 , xn을 곱해야하니 1번의 곱하기 발생
xn-1 = gn-1 - un-1n*xn / un-1 , xn-1을 구하기 위해 1번의 나누기가 발생한다.
step2도 이렇게 구할 수 있고

를 유도할 수 있다.
이를 종합해서

를 유도할 수 있다.
이게 왜 중요한가?
만약 A->U로 변환이 완료된 상태라면 n^2만으로 해를 구할 수 있다.
A^-1b 를 구해보자.
A^-1을 안다고 가정할 때
Ax = b
A^-1Ax = A^-1b
x = A^-1b
를 통해 x를 구하면 n^3번의 곱하기가 발생한다. (행렬곱의 cost)
U를 구해놓았다면 n^2의 곱하기를 통해 해를 구할 수 있다.
b가 n*n행렬이라고 가정한다면 A^tb는 n^3으로 풀리고
U를 구해놓은 경우도 n* n^2으로 동일한 계산량으로 풀 수 있다.
가우스 소거법 절차)

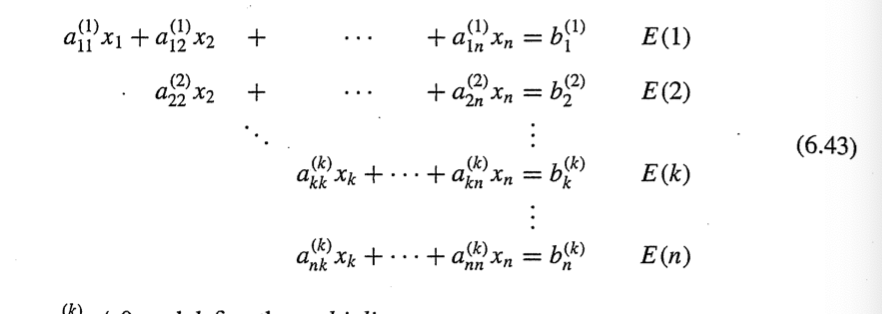
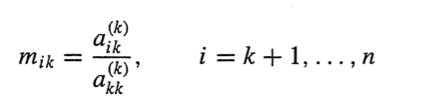

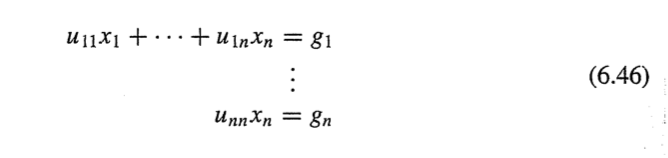
그림으로 이해하는게 더 빠름

———————————
LU분해
이전 과정을 통해 미리 계산해주는게 연산속도를 빠르게할 수 있음을 알았다.
해결된 선형 시스템의 계수 행렬은 2개의 삼각행렬로 나타낼 수 있다.
가우스 소거법의 6.42~6.45과정을 통해 Ux = g 로 나타낼 수 있다.
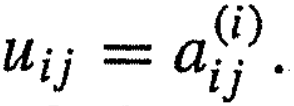

또 L은 Multipliers이 된다.
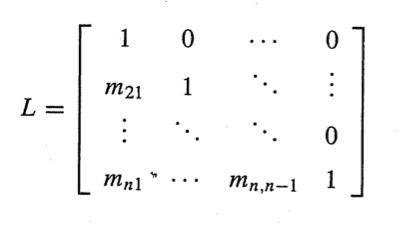
LU = A
1행을 살펴보면
u11
m21u11
m31u11
..
….
가 되는걸 알 수 있는데
생각해보면 U를 만들때 m을 a11에 곱해서 substrct했던걸 생각하면
m21u11 = a21
m31u11 = a31
…
임을 알 수 있다.
LU분해를 실제 적용해보자.
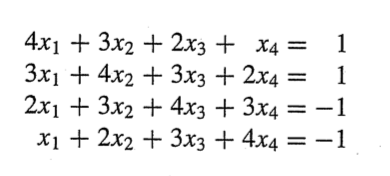

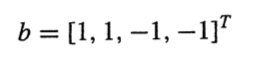
L에서 a1부터 대입하여 g를 빠르게 구할 수 있다. (b->g 로 변환 )
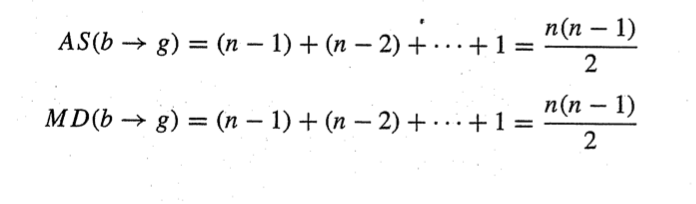

Ux = g (g->x로 변환)
마지막 항부터 대입하여 x를 빠르게 구할수 있다.
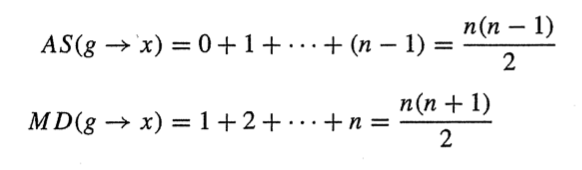

——————
compact variannts of gaussian elimination (콤팩트 변형)
LU분해를 공식화 하자

이상태에서 일반 행렬곱으로 바라보는게 직관적이고 쉽게 식을 유도할 수 있다.
ex) a11 = 1*u11 + 0*0 + 0*0

이를 doolittle’s method (두리틀 방식)이라고 한다. (LU분해하는 다른 방법은 가우스 소거법)
두리틀 방식과 LU 분해는 연산 속도는 같은데 큰 차이가 있다.
바로 rounding errors 를 줄일 수 있다. (조금의 비용증가가 있음)
만약 우리가 single precision(float)으로 값을 저장했다면 double pricision을 사용했을때 오차를 훨신 줄일수 있다. 따라서 double pricision으로 곱하고, 합한 후 single precision으로 값을 반환한다면 single precision을 쓸때보다 더 적은 에러를 가질 수 있게된다.
가우스 소거법은 2/3n^3 , 두리틀은 n^2 만큼 오차를 줄일수있다.
또다른 문제 : 메모리는 어떻게 줄일까?
그냥 있던 자리 그대로 차지하면 된다.
mik 가 있다면 i>k 에대해 A(i,k) 에 두고
uij가 있다면 i<=j 에 대해 A(i,j) 에 두면 된다.
—————
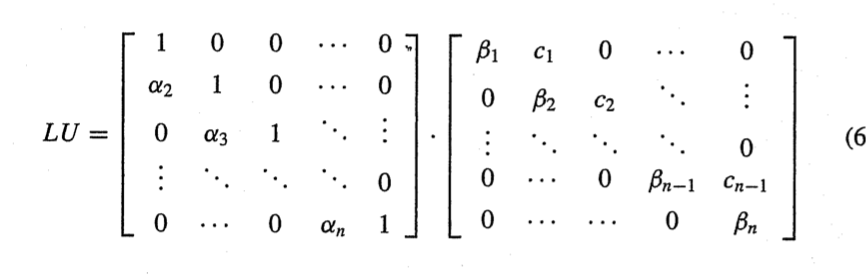
tridiagonal system
계수행렬 A가 특이한 형태를 가질때 가우시안 소거법을 단순하게 만드는게 가능하다.
Ax = f

근사같은 수 분석 분야에서 tridiagonal system이 자주 사용된다.
현실 문제에서도 이걸 쓰는데 우리는 스플라인 보간법이 이러한 예시였다.
이게 왜 단순화가 되는가?
mij가 대부분 0이다.
또 U의 대부분이 0이다.
일반화
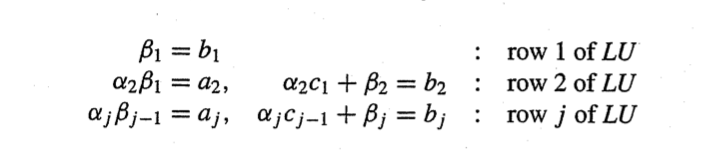
이것도 행렬곱으로 자리를 정하고 보는게 더 직관적이다.
a2 = 알파2*베타1 + 1*0 + 0*0 + 0*0 …..
위의 식을 알파와 베타에 관해 정리하면 다음 식을 얻을 수 있다.
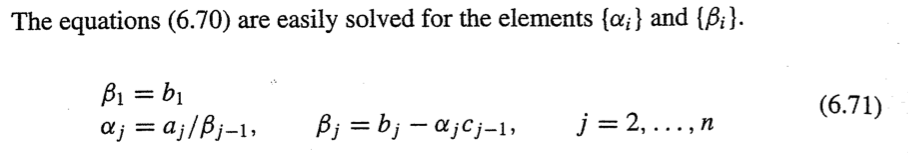
이제 LU분해를 해보자
LUx = f
Lg = f
Ux = g
아까와 같이 Lg = f 단계에선 처음 요소부터 대입해서 얻으면되고(L의 첫 항은 1이니까 그냥 바로 얻을 수 있음)
Ux = g 에선 끝 요소부터 대입해서 값을 얻으면 된다.
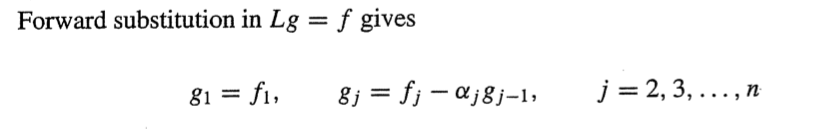
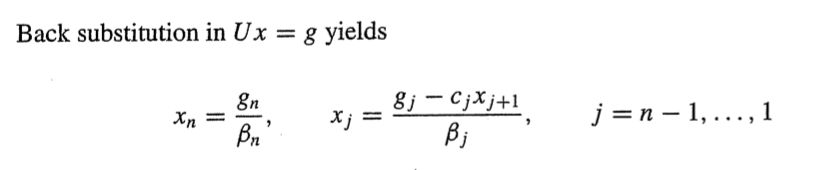
이러한 특성을 만족한다.
연산 횟수 계산하기.
5n-4개의 곱하기와 나누기를 사용하게 된다.
why?
A 에서 LU로 분해할때 첫행 이후 각 단계마다 1번의 나누기와 곱하기 발생
0 2 2 2…
2(n-1)
Lg = f 에서 첫 요소가 g1이고 g1에 multiplier 곱한거 빼서 g2 얻고 …
0 1 1 1 …
n-1
Ux = g 에서 맨끝항은 gn에 베타n로 나누고 그 이후는 c와 gn곱을 뺀거에 베타 n-1 나누기 반복
1 2 2 2 ….
2n-1
따라서
5n-4 개의 곱하기 나누기 연산 발생

이부분을 LU로 분해
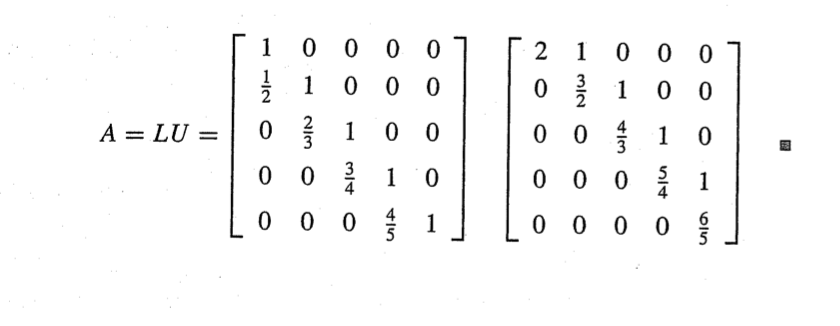
앞선 예제는 피벗팅을 고려하지 않았음.

양 끝에 있을땐 a와 c의 절대값보다 더 커야함.
j일땐 대각 성분의 절대값이 a와 c의 절대값 합보다 항상 크거나 같아야함.
이러한 상황에서 대각 성분이 0과 가까워지지 않음.
tridiagonal matrix는
대부분이 0과 가까운 희소행렬에 속하는 특이한 케이스이고
이러한 희소행렬에 대해 가우스 소거법의 효율적인 확장이 이루어질 수 있음.
———