2023. 10. 24. 01:28ㆍ빅데이터 수학 기초
차원의 저주
ex1 ) 분류 문제

각 영역을 분류하는 문제인데 어떻게 분류되는지 이해할 수 없음
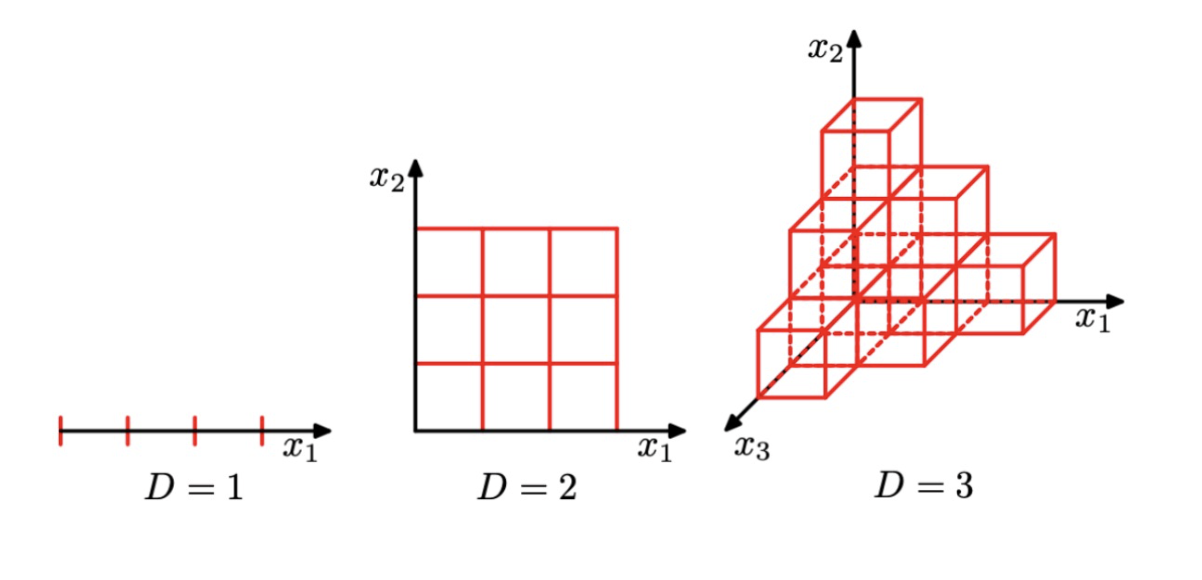
1차원에서 3등분을 나누면 그냥 3등분이 나눠지는건데
이차원에선 3등분하면 9개의 공간이 나오고 3차원에서 3등분하면 27개의 공간이 나옴.
맘대로 나누지 못함.
ex2) point간 거리
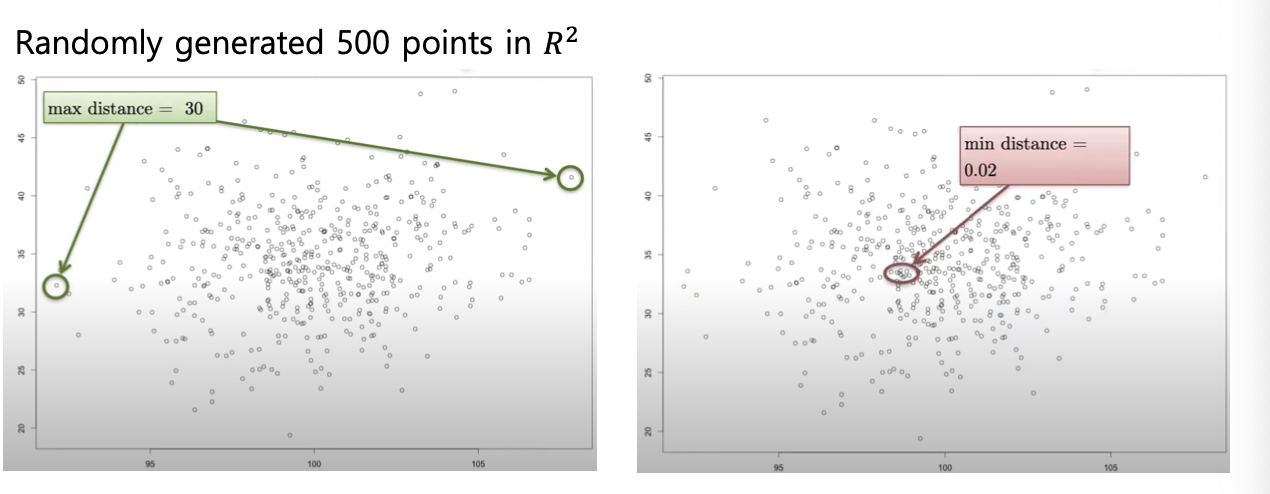

차원이 높아질수록 가장 가까운 곳과 먼 곳의 거리가 0에 수렴하게 됨.
ex3) cosine similarity
두 벡터간 유사도를 구하는 방법으로 내적과 벡터의 크기를 나누는 방법이다.

해당 기법을 사용하면 [-1,1] 구간의 값이 나온다. 직교일때 0 (cos π/2 = 0), 벡터의 각도에 의존한다는 특징이 있는 기법이다.
차원이 높아질수록 이 기법을 사용할 때
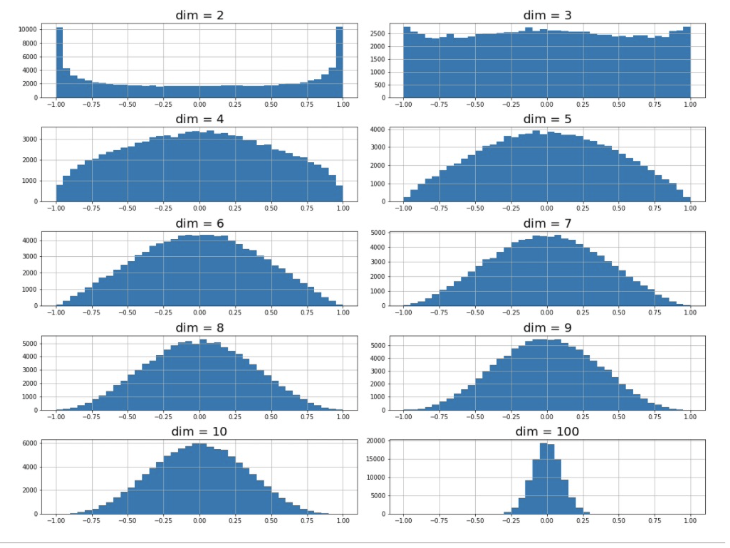
차원이 높아질수록 벡터간의 유사성이 사라져간다.
ex4) 공의 부피
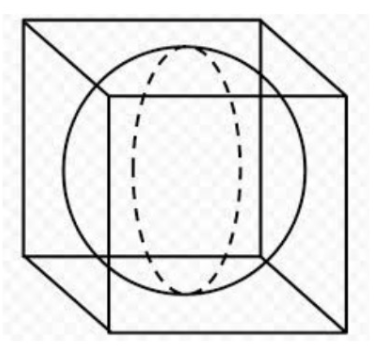
차원이 높아질수록 공의 부피가 0에 수렴해진다.
차원의 축복
ex1 ) 고차원일수록 아무렇게나 만든 두 벡터가 orthogonal 하고 랜덤으로 만든 n by n random matrix이 가역적이게 된다.
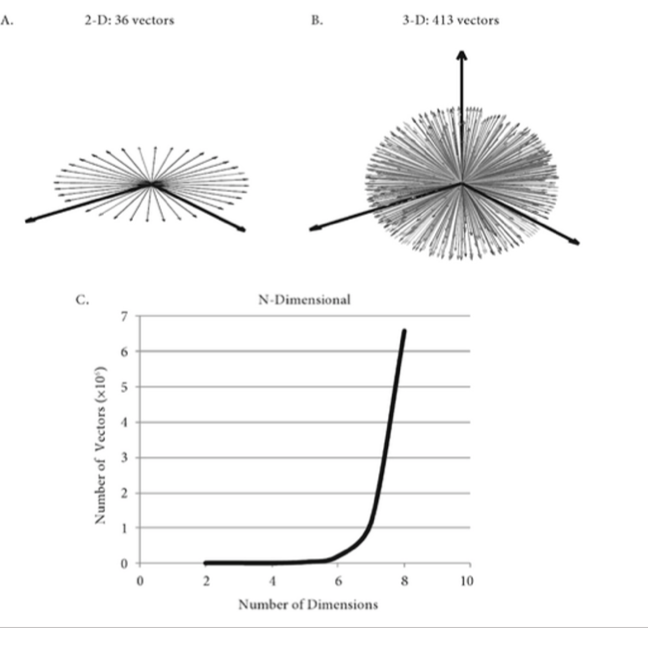
ex2 ) 고차원에서 아이젠벨류를 구해봤더니 원안에 모임.
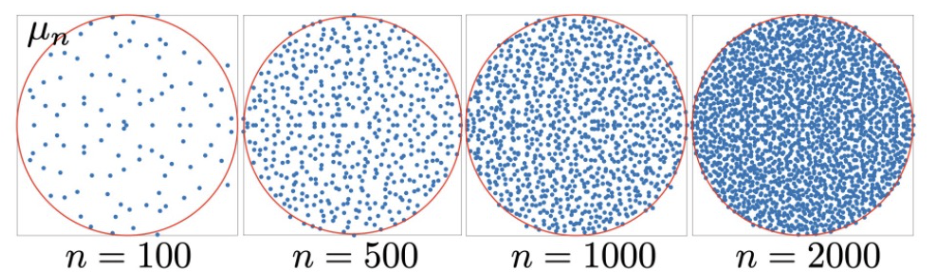
entropy
정보를 정량화하는 방법론(자주 보내지는 정보는 가치가 떨어진다 등.)
Shannon entropy

이산 확률 변수 X ( sum(X) = 1, xi > 0) 에 대해 위의 식이 성립한다.
정보의 양을 질문의 개수로 측정!
동등한 확률로 정보를 생산하는 기계, 동등하지 않은 확률로 정보를 생산하는 기계 중 무엇이 더 가치 있는 정보를 생산할까?
확률이 같다면 정보의 가치가 높아진다. (뭐가 나올지 확률이 비슷하니까 예측하기 어려움.)
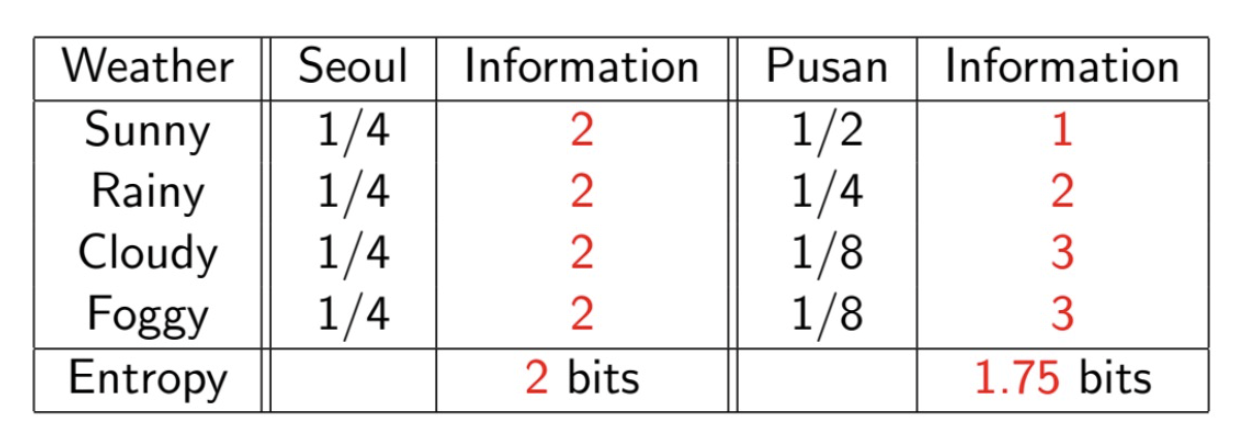

첫번째 질문의 답은 0이다 why? 질문을 하지 않아도 1인걸 알 수 있다.
두번째 질문의 답은 logk 이다. -> k * (1/k logk) = logk
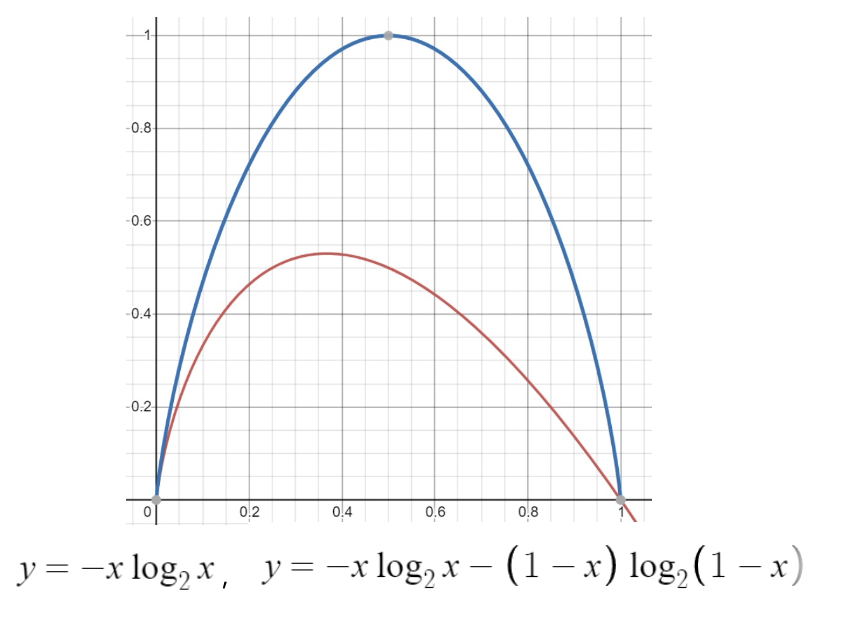
파란색의 함수가 x, (1-x) 의 엔트로피를 합친 그래프이다.
x1,x2,1-x1-x2 의 엔트로피의 그래프는 3차원 상 (1/3,1/3,1/3) 의 값이 1이고 최대값인 그래프이다.
joint entropy
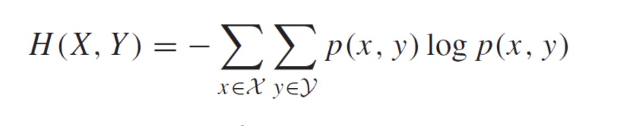
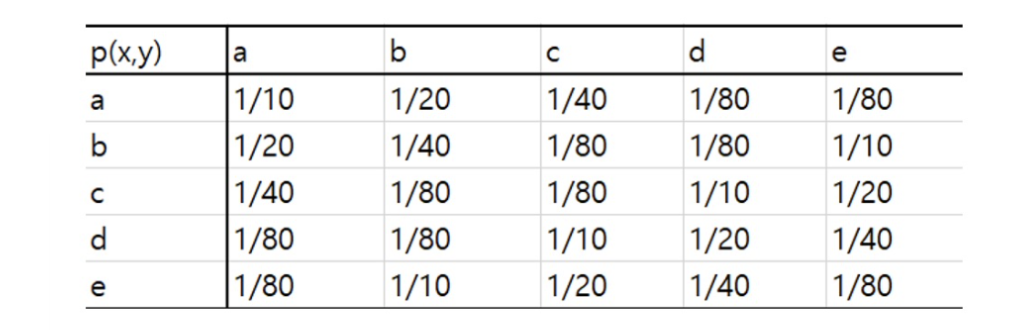
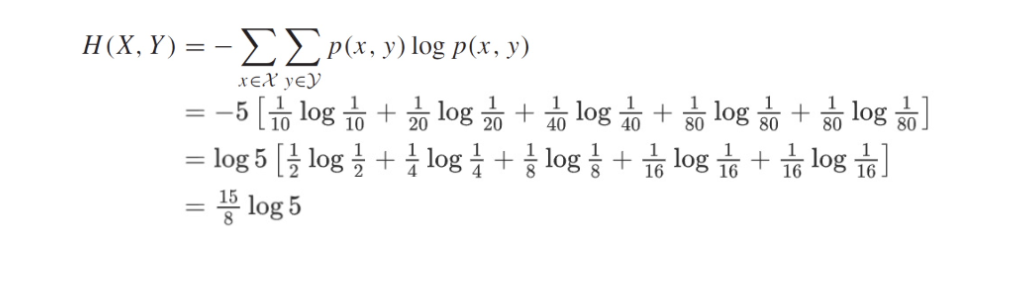
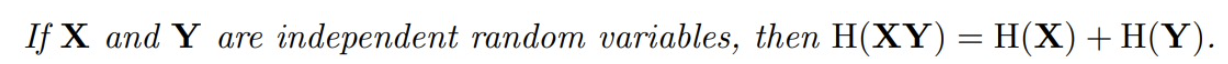
X와 Y가 독립일때 분리할 수 있다.
cross entropy
서로 다른 분포 p와 q에 두 확률 분포 p,q 에 차이를 알기위해 사용한다.
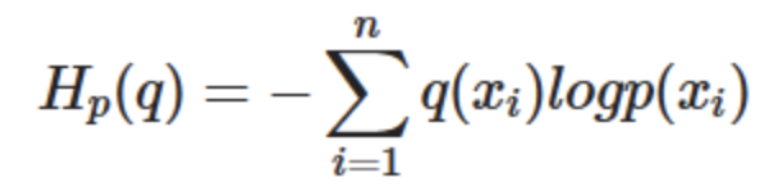
크로스 엔트로피는 인공지능에서 실제 값과 비교할때 모델이 예측한 값이 얼마나 잘 예측했는가에 대한 지표로 쓰일 수 있다.
우리는 훈련 데이터로 무작위로 x 음식에 대한 선호도(좋음 , 보통 , 싫음)이 0.8, 0.1 , 0.1 비율로 존재한다는 걸 안다.
인공지능이 초기 값으로 0.2 , 0.2 , 0.6 비율로 존재한다고 가정했다. 이때 cross entropy가 1.5 임을 알게됬다.
이를 지표가 최소화가 되도록, 경사하강법을 사용해 최적의 파라미터를 찾아낼 수 있게 된다.
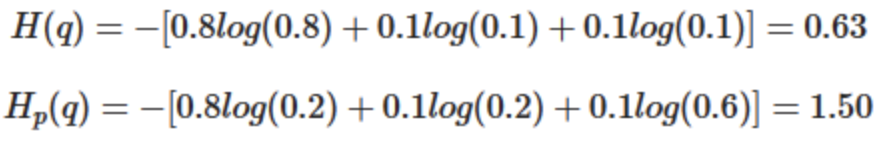
KL divergence

크로스 엔트로피만으로는 실제 샤논 엔트로피와의 차이가 어느정도인지 직관적이지 않으니 이 둘을 빼자!
초보를 위한 정보이론 안내서 - KL divergence 쉽게 보기
사실 KL divergence는 전혀 낯선 개념이 아니라 우리가 알고 있는 내용에 이미 들어있는 개념입니다. 두 확률분포 간의 차이를 나타내는 개념인 KL divergence가 어디서 나온 것인지 먼저 파악하고, 이
hyunw.kim
요약하자면 젠슨 부등식으로 KL divergence 가 항상 0보다 크고 역이 성립하지 않아 거리의 개념이 아니다.
그밖에도
조건부 엔트로피
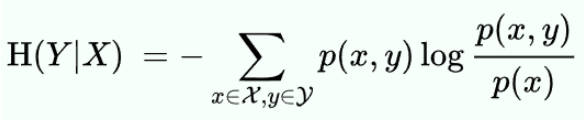
Mutual information 등 여러 엔트로피가 있다.
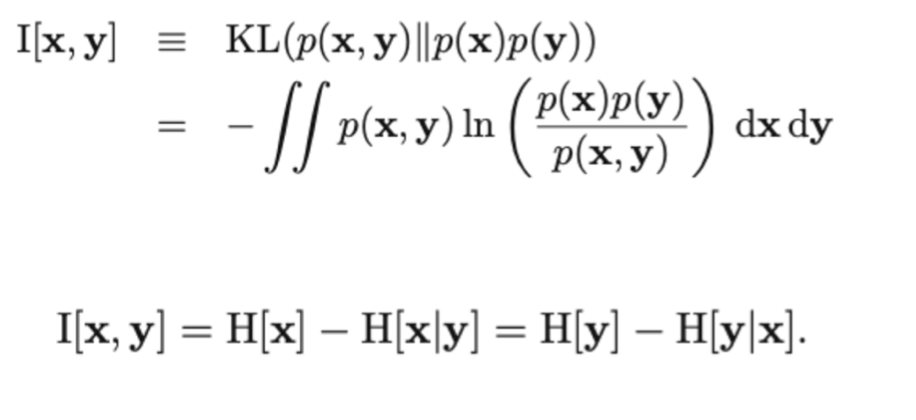
'빅데이터 수학 기초' 카테고리의 다른 글
| 빅데이터 선형대수학 (1) | 2023.10.23 |
|---|---|
| 데이터 (1) | 2023.10.23 |
| 빅데이터 수학 기초론 문제풀이 week7 (0) | 2023.10.22 |
| 빅데이터 수학 기초론 문제풀이 week6 (0) | 2023.10.22 |